Synkronsvømming er ikke bare en olympisk gren. Putt noen hundre fisk av det rette slaget i en tank, så kan resultat bli synkronisert svømming i stor skala. Det starter gjerne kaotisk, med småskremt fisk pilende i alle retninger. Men temmelig snart opphører kaoset og fiskene ender opp svømmende rundt i ring–som en roterende galakse i miniatyr, bare av fisk. Og akkurat som i barnesangen: De svømmer og de svømmer og de svømmer rundt…i alle fall helt inntil et par fisk bryter ut av gruppen og skyter fart mot andre siden av tanken. Da bråvender hver eneste fisk og følger etter, og plutselig flyter hele stimen avgårde i en parallel formasjon som gardens drillkorps knapt kunne gjort bedre. Men tanken er ikke bygd for kolonner av marsjerende fisk og ubønnhørlig går fronten av stimen rett inn i veggen. Det bryter opp mønsteret og kaos er tilbake. Og slik fortsetter en fiskedag.

Sett utenfra er det merkelig og fascinerende å se hvordan stimen av fisk organiserer seg selv. Det går fra hulter og bulter til ringformasjon, og derfra til nesten krystallinsk orden når de svømmer parallelt. Det skjer momentant, og det skjer uten ytre påvirkning. Det finnes ingen dirigent som sørger for å gi hver eneste fisk klarsignal til å svinge til høyre, eller til venstre, eller å skyte fart. Antagelig har en fisk heller ikke oversikt over stort mer enn hva de nærmeste nabofiskene gjør, og det er den informasjonen den må basere seg på når den avgjør hvor ferden går videre. Allikevel er dette nok til at gruppen kan opptre samkjørt med høy grad av koordinasjon.

For å utvikle en forståelse av hva slags regler fisk (eller andre biologiske systemer, som celler, sau, eller mennesker) følger når de beveger seg er det helt nødvendig å gjøre visse forenklinger. Som for eksempel at fisken ikke lenger er en sølvskimrende, elegant skapning som basker seg framover i forholdsvis diskrete skritt med halefinnen. I stedet kan vi la fisken være representert som et matematisk punkt, med koordinater i x- og y-planet som flytter seg omkring i selskap med andre punkter etterhvert som tiden går. Dette innskrumpede bildet av virkeligheten gjør det mulig å betrakte en gruppe av fisk som et partikkelsystem, og da er veien til fysikken og Newtons lover kort.

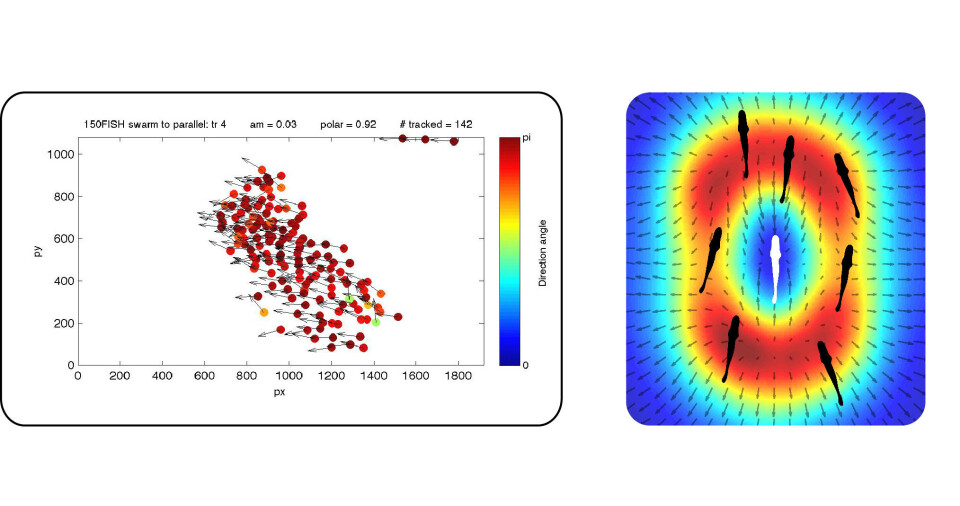
Det finnes selvfølgelig ingen spesifikk lov for fiskestimer, men Newtons andre lov, som sier at kraft er lik masse ganger akselerasjon, brukes ofte for å formulere modeller for kollektiv bevegelse. Newtons andre lov kan derfor også hjelpe oss med å besvare spørsmålet vi stiller oss i vår forskning: Kan vi, ved å måle fiskens bevegelser over tid, forstå hva slags modell som best beskriver en stim av fisk?

I de undersøkelsene vi har ferdigstilt så langt har vi undersøkt systemer av to og tre fisk. Fordelen med å starte med så små grupper — det kan knapt kalles stimer – er at det er enklere å vriste ut hvordan fisk reagerer på hverandres oppførsel. Ved å måle hver fisks posisjon, hastighet og akselerasjon er det mulig å få et omtrentlig bilde på hvordan en fisk vil reagere i en gitt situasjon. For eksempel er det slik at når en fisk kommer litt for tett på en annen fisk bakfra, er det mest sannsynlig at den bremser ned eller gjør en unnamanøver, mens fisken som ligger foran gir litt ekstra gass. I grunnen ganske likt som når vi kjører bil.

Men holder det med en enkel repulsjons- og attraksjonskraft for å genere de ulike formene en fiskestim kan ta? Teoretiske studier har vist at vi kan få ringformasjoner i systemer av selvgående partikler som tiltrekker hverandre på langt hold og frastøtes når de kommer for nære. Men de modellene er svært stabile, og har ofte en nesten krystallin struktur. Det er ikke tilfelle med fisketypen vi kikker på. Til tross for at den viser sterke elementer av organisering, ligger ikke fisken og vaker i gitterformasjoner. Tvert i mot glir fiskene forbi hverandre og bytter posisjon ofte. Utfordringen framover blir derfor å forstå hvordan en stim kan framstå som velordnet selv om det er sterke svingninger lokalt. Og kanskje betyr det at Newtons lover for fiskerstimer ikke er det endelige svaret for hvordan vi best kan forstå kollektiv bevegelse.

Aktuell litteratur:

Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study

Inferring individual rules from collective behavior

Inferring the structure and dynamics of interactions in schooling fish

Inferring the rules of interaction of shoaling fish