Er det sånn at hyppige, konkrete og faglige tilbakemeldinger fra læreren er det som gjør at elevene lærer best? Dette virker kanskje som en opplagt sannhet - for hvorfor skulle elevene lære av å få sjeldne, vage eller ikke-faglige tilbakemeldinger? Men jeg tror ikke det stemmer. I hvert fall ikke alltid. Fra egen praksis som matematikklærer har jeg mange moteksempler. Jeg tror altså jeg kan vise til situasjoner der elevene lærer mindre hvis jeg hadde kommet med en konkret faglig tilbakemelding, enn hvis jeg hadde latt være. La oss ta et eksempel:

Studer figuren på bildet under:

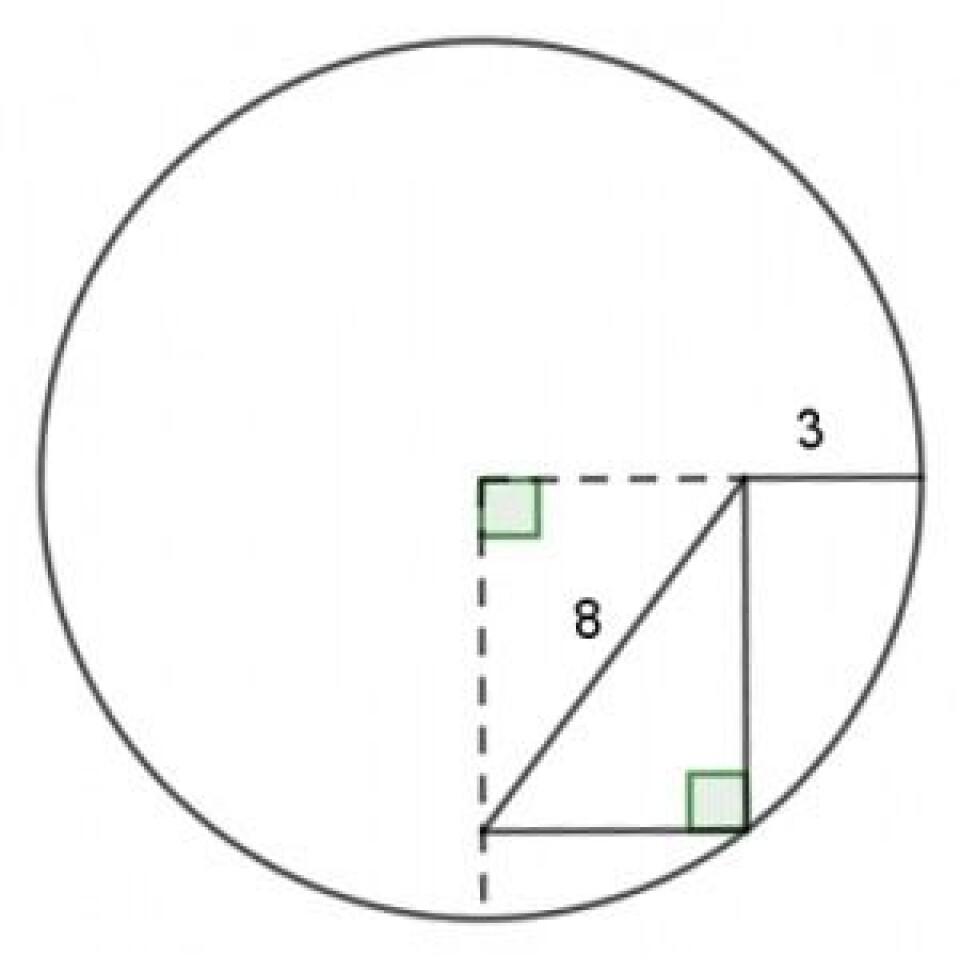
Klarer du å finne ut hva radius i sirkelen er?

Denne oppgaven har jeg gitt på mange alderstrinn – fra sent på barneskolen til universitet – og alle grupper reagerer forskjellig. De yngste gjetter vilt («det må være syv!») eller tegner videre på tegningen. De litt eldre elevene setter opp Pytagoras’ likning og skjønner at de ikke har nok informasjon til å løse likningen. Matematikere visualiserer at man endrer størrelsen på sirkelen uten å endre lengdene og vinklene; de håper å vise elegant at oppgaven har flere løsninger. Rundt en fjerdedel ser umiddelbart løsningen; de ser at diagonalen i rektangelet har lengde 8 og tegner opp den andre diagonalen. Denne diagonalen vil være radius i sirkelen, så svaret er 8. Ser du det? For en tilfredsstillende løsning!

Like sikkert som at løsningen er tilfredsstillende er at det er vanskelig for en lærer å gi tilbakemeldinger og støtte på denne oppgaven som elevene lærer noe av. Læreren kan gi en konkret fremovermelding som «forsøk å tegne den andre diagonalen!», men tror vi elevene blir bedre problemløsere av å bli gitt svaret på denne måten? Kanskje, kanskje ikke. Jeg tror tilbakemeldingen er for konkret så elevene ikke må tenke seg hardt nok om, og man kan ikke lære seg matematikk uten å tenke seg hardt om av og til. Kanskje bør man gi en vagere tilbakemelding med mindre faglig innhold, slik som «nå har du kjørt deg fast med de likningene, prøv å tenke på andre måter» eller «jeg hjelper deg ikke ennå, det er jo bare gått 5 minutter! Du må prøve litt til.» Vil elevene lære noe mer av disse tilbakemeldingene?

 Eksempelet peker på problemer ved å gi «hyppige, konkrete og faglige tilbakemeldinger» i matematikklasserommet. Kanskje må ikke tilbakemeldinger gis så ofte, fordi elever må få streve litt. Kanskje må graden av konkrethet og faglighet tilpasses oppgavetypen og formålet med oppgaven. Hvis formålet er å automatisere regnemetoder trenger man kanskje hyppige og konkrete tilbakemeldinger slik at elevene ikke automatiserer en gal regnemetode. Hvis oppgaven er ment å gjøre elevene til gode problemløsere eller å utforske et nytt begrep bør kanskje tilbakemeldingene være helt annerledes.

Jeg ønsker å finne ut om norske matematikklærere gjør disse tilpasningene. For å finne ut av det skal jeg systematisk studere de nesten 200 matematikktimene som er videofilmet til LISA-prosjektet. Akkurat nå titter jeg på film og kategoriserer alle tilbakemeldinger læreren gir elevene sine på forskjellige oppgavetyper og hvordan elevene reagerer. Vil jeg finne at norske lærere støtter elever i å tenke hardt og lenge på vanskelige oppgaver? Tilpasser lærerne tilbakemeldingen til oppgavetypen? Hva slags type oppgaver velger lærerne å gi? Og hvordan undersøker man egentlig dette systematisk i nesten 200 matematikktimer? Noen svar (og mange flere spørsmål) får du i denne bloggen.

Roar Bakken Stovner er stipendiat ved Institutt for lærerutdanning og skoleforskning på Universitetet i Oslo. I sitt doktorgradsprosjekt ser han på læreres tilbakemeldinger i matematikktimer og betydningen for læring.