Se for deg at du står på en stor slette. I det fjerne ser du en gruppe dyr bevege seg mot deg. De er så langt unna at de bare skimtes som prikker mot horisonten. Du snur deg og kikker mot plassen der turfølget ditt er i ferd med å slå leir. Raskt og nesten ubevisst anslår du at hvis dette er farlige og kampklare dyr, vil hver person i turfølget måtte nedkjempe flere dyr ved en eventuell konfrontasjon. Det er på tide å komme seg vekk.

Selv om dette heldigvis er et tenkt scenario, illustrerer det en livsviktig ferdighet du kanskje ikke har tenkt over at du har. I likhet med en del andre dyr, er nemlig vi mennesker ganske gode til å estimere mengder og å ta raske beslutninger om hvilken av to mengder som er størst, selv når vi ikke har anledning til å telle. Denne ferdigheten, kalt «approximate number sense» på engelsk, kan vi tenke på som en instinktiv omtrentlig mengdeforståelse.

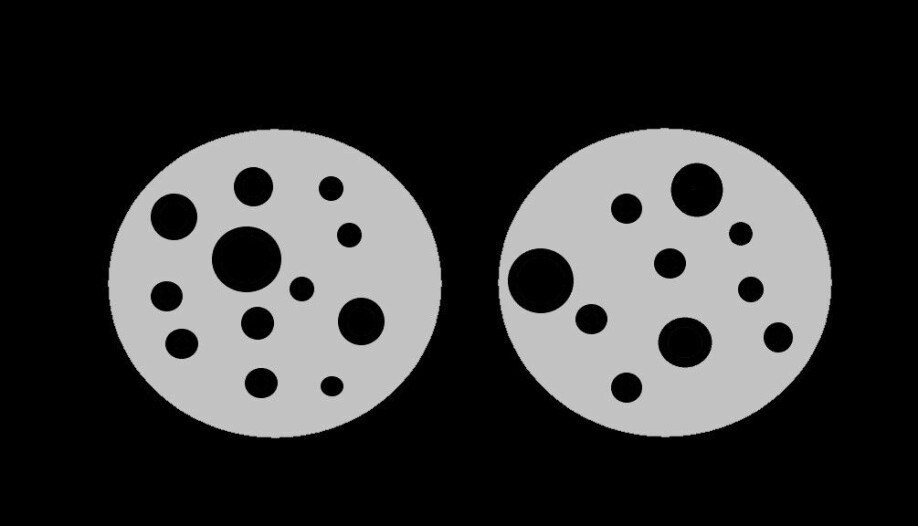
Forskere har funnet ut at det går an å måle hvor raskt og nøyaktig mennesker kan estimere mengder på denne måten, ved å be deltakere i eksperimenter om å velge mellom illustrasjoner som viser et ulikt antall prikker. Og jo større forskjell det er på antallet prikker på bildene, jo raskere klarer man å bedømme hvor det er flest.

På automatikk kan de fleste ta særdeles raske og riktige beslutninger i denne typen oppgaver, uavhengig av formatet mengdene presenteres i. Men overraskende nok er det ikke bare voksne som er ganske presise i sin estimering av mengder!

Kan babyer regne?

For å finne ut hvor tidlig i livet vi mennesker klarer å skille mellom størrelser av mengder, har forskere gjennomført varianter av disse eksperimentene med småbarn og babyer som deltakere.

I et klassisk studie fra 1992, viste psykologen Karen Wynn at babyer på 4 måneder hadde forventninger til utfallene av enkle regnestykker, som 1 + 2. For når disse regnestykkene ble demonstrert med små gjenstander, uttrykte babyene overraskelse hvis de fikk se et uriktig – og dermed uventet – utfall.

Også gjennom hørselen kan små barn instinktivt oppfatte mengder. Nyfødte som får se flere samlinger med fargerike figurer, kikker spontant på samlingen som samsvarer med antallet lyder de får høre avspilt i en sekvens.

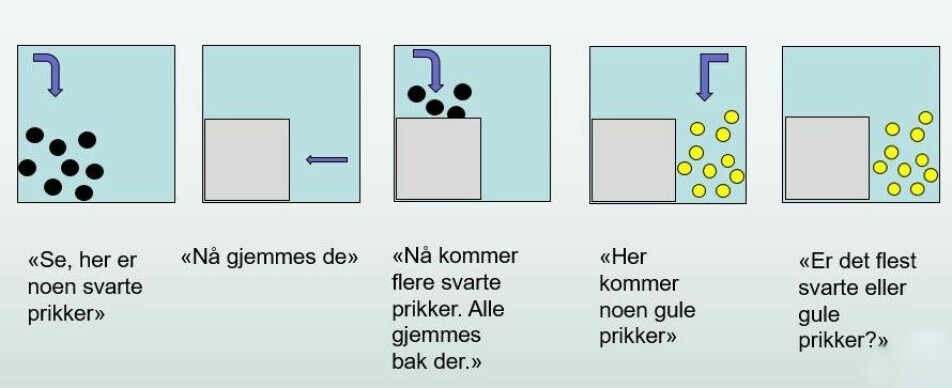
Ikke bare er disse funnene bekreftet i en rekke andre studier, men det er også gjort lignende funn med bruk av mer komplekse oppgaver som omfatter omtrentlig regning. I et nyere studie med førskolebarn, viste et forskerteam på Harvard University en animasjon til barna som deltok. I animasjonen ble først noen svarte prikker vist på skjermen, og deretter dekket over av en figur. Et nytt sett med svarte prikker kom til syne og forsvant deretter bak den samme figuren. Til slutt ble det vist en ny samling gule prikker, og barna ble spurt om det til sammen var flest svarte eller gule prikker. Barna hadde ikke tid til å telle og kunne ikke se de svarte prikkene samtidig, men gav likevel riktig svar i de fleste tilfellene. Med andre ord gjorde de en omtrentlig sammenslåing av prikkene de så i to ulike omganger, og sammenlignet den totale mengden med den siste mengden av gule prikker som ble vist.

Med så solide bevis for at vi både estimerer og regner med omtrentlige mengder fra vi er helt små, skulle man kanskje tenke at også matematikken vi lærer på skolen og bruker i arbeidslivet også er ganske instinktiv?

Instinktiv versus lært matematikk

Vår tidligste form for tallprosessering er oppfattelsen og manipuleringen av omtrentlige mengder som illustrert av studiene over. Denne ferdigheten skiller seg fra den senere matematikken i det at den ikke involverer tallsymboler, at den ser ut til å være lik på tvers av kulturer og at den blir mindre nøyaktig jo større mengder det er snakk om. Tallsystemet vi lærer når vi teller og regner med symboler er derimot abstrakt, kulturelt forankret og avansert nok til å brukes i kompliserte matematiske problemer. Dermed er det ikke sånn at det vi lærer er en direkte forlengelse av våre medfødte matematiske evner. Men det er uten tvil en sammenheng!

En rekke studier viser nemlig at de som er raske på mengde-estimering også ofte har gode formelle regneferdigheter. I tillegg er de samme områdene i hjernen aktive hos spedbarn som ser på ulike mengdestørrelser og hos voksne når de vurderer både symbolske og ikke-symbolske størrelser – det vil si både tallsymboler og mengder. Disse resultatene kan tolkes som at estimeringsferdigheter over tid bidrar til utviklingen av mer avansert matematisk forståelse som aktiverer samme del av hjernen.

Funnene har dannet grunnlaget for en intens debatt i feltet om hvor tett den instinktive matematikken henger sammen med den vi møter på skolebenken.

Blir matte enkelt hvis du trener på mengdeanslag?

Ettersom sammenhengen mellom disse medfødte omtrentlige regneferdighetene og formell matematikk er så tydelige, har mange forskere håpet på at trening med mengder og estimering vil kunne gi større mestring i matematikkfaget. Dessverre har treningsopplegg av denne typen foreløpig ikke gitt noen entydige resultater.

Dessuten viser studier som går over tid, at det ikke bare er en sammenheng mellom tidlig mengdeforståelse og senere matematikkferdigheter, men også omvendt – mellom matematikkferdigheter og senere mengdeforståelse. Dermed kan vi konkludere med at systemene henger sammen, men at du ikke nødvendigvis bør trene på mengde-estimering for å bli bedre på å regne med tallsymboler.

Likevel tyder noen funn på at vår medfødte mengdeforståelse kan være et viktig ledd i koblingen mellom mengder og tallsymbolene som representerer disse mengdene. Og kanskje det er det som er utslagsgivende for sammenhengene man har oppdaget mellom mengdeforståelse og mer avanserte deler av matematikken som krever symboler, regler og et eget språk.

Det som er sikkert, er at vi fra evolusjonens side er utstyrt med et nyttig system som hjelper oss med å vurdere farer som flokker av ville dyr og mengder av ressurser som mat og materialer. En slik medfødt evne til å anslå mengder som er viktige for vår overlevelse, kan være én bit av grunnlaget for å utvikle en god forståelse av tallsystemet. Men abstraksjonene vi må gjøre for å benytte oss av vår moderne matematikk, krever likevel eksplisitt opplæring og mye trening for de aller fleste.

Kilder:

Barth, H., La Mont, K., Lipton, J., & Spelke, E. S. (2005). Abstract number and arithmetic in preschool children. Proceedings of the national academy of sciences, 102(39), 14116-14121.

Brannon, E. M., & Merritt, D. J. (2011). Evolutionary foundations of the approximate number system. Space, time and number in the brain, 207-224.

Gilmore, C. (2013). Approximate arithmetic abilities in childhood. In The Oxford handbook of numerical cognition.

He, Y., Zhou, X., Shi, D., Song, H., Zhang, H., & Shi, J. (2016). New evidence on causal relationship between approximate number system (ANS) acuity and arithmetic ability in elementary-school students: a longitudinal cross-lagged analysis. Frontiers in psychology, 7, 1052.

Izard, V., Sann, C., Spelke, E. S., & Streri, A. (2009). Newborn infants perceive abstract numbers. Proceedings of the National Academy of Sciences of the United States of America, 106, 10382– 10385.

Pica, P., Lemer, C., Izard, V., & Dehaene, S. (2004). Exact and approximate arithmetic in an Amazonian indigene group. Science, 306(5695), 499-503.

Wynn, K. (1992). Addition and subtraction by human infants. Nature, 358(6389), 749-750